¿Qué es un polinomio?
Un polinomio es una expresión matemática que consta de variables, coeficientes y operaciones de suma, resta, multiplicación y exponentes enteros no negativos.
Los polinomios son una parte importante del “lenguaje” de las matemáticas y el álgebra. Se utilizan en casi todos los campos de las matemáticas para expresar números como resultado de operaciones matemáticas. Los polinomios también son “bloques de construcción” en otros tipos de expresiones matemáticas, como las expresiones racionales.
Muchos procesos matemáticos que se realizan en la vida cotidiana se pueden interpretar como polinomios. La suma del costo de los artículos en una factura de supermercado se puede interpretar como un polinomio. El cálculo de la distancia recorrida por un vehículo u objeto se puede interpretar como un polinomio. El cálculo del perímetro, el área y el volumen de figuras geométricas se puede interpretar como polinomios. Estas son solo algunas de las muchas aplicaciones de los polinomios.
Algunas de las expresiones que vemos a continuación son polinomios (en azul) y otras no (en rojo). Los polinomios se pueden identificar observando qué expresiones contienen solo las operaciones de suma, resta, multiplicación y exponentes enteros no negativos. Las expresiones no polinomiales serán las expresiones que contengan otras operaciones.
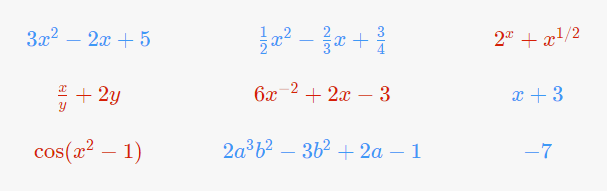
Un polinomio es una expresión algebraica compuesta por una suma o diferencia de términos, cada uno de los cuales es un producto de un número real (llamado coeficiente) y una potencia de una variable (llamada variable independiente).
La variable independiente puede ser x, y, z, etc. y su exponente es un número entero no negativo. El grado de un polinomio es el mayor exponente de la variable independiente. Ejemplos de polinomios son:
2x + 3 es un polinomio de grado 1
3x^2 + 2x – 1 es un polinomio de grado 2
4x^3 + 3x^2 – 2x + 1 es un polinomio de grado 3
Los polinomios también pueden tener un grado cero, es decir, solo un término constante. Ejemplo:
7 es un polinomio de grado cero.
Ejemplos de sumas con polinomios
(2x^2 + 3x – 4) + (x^2 – 2x + 1) = 3x^2 + x – 3
(4x^3 + 2x^2 – 3x + 5) + (-2x^3 + 3x^2 + 2x – 7) = 2x^3 + 5x^2 – x – 2
(3x – 2) + (5x + 4) = 8x + 2
Recuerda que para sumar polinomios, debes sumar los términos con el mismo exponente.
Ejemplos de resta con polinomios
(2x^2 + 3x – 4) – (x^2 – 2x + 1) = x^2 + 5x – 5
(4x^3 + 2x^2 – 3x + 5) – (-2x^3 + 3x^2 + 2x – 7) = 6x^3 – x^2 – 5x + 12
(3x – 2) – (5x + 4) = -2x – 6
Para restar polinomios, debes restar los términos con el mismo exponente.
Es importante recordar que se restan los coeficientes de los términos con el mismo exponente, no se resta el exponente.
(2x^2 + 3x – 4) * (x – 2)
Para multiplicar polinomios, debes multiplicar cada término del primer polinomio por cada término del segundo polinomio, y luego sumar los productos obtenidos con los mismos exponentes. La ecuación es la siguiente:
(2x^2 + 3x – 4) * (x – 2) = 2x^3 – 4x^2 + 3x^2 – 6x – 8x + 8
= 2x^3 – x^2 – x + 8
Es importante recordar que la regla distributiva se utiliza en cada uno de los términos del polinomio. Este proceso de multiplicar polinomios es similar a como se multiplican los binomios.
Espero que esto te ayude a entender cómo se multiplican los polinomios. Si tienes alguna pregunta adicional, no dudes en preguntar.
Los polinomios a menudo se clasifican por grado.
El grado de un monomio es la suma de los exponentes de cada variable en el monomio.
El grado de un polinomio es el mayor grado de todos los grados de monomios en el polinomio.
Suma y resta
Los polinomios se pueden sumar bajo la ley asociativa de la suma.
Hay dos polinomios: (3x² – 2x + 4) y (-3x² +6x -10)
(−3x 2 +6x−10) ¿Cuál es la suma de estos polinomios?
Combinando términos semejantes, la suma resultante es 4x−6
Ejemplos de división con polinomios
Dividir (4x^3 + 2x^2 – 3x + 5) entre (x – 2)
Para dividir polinomios, se utiliza el método de la división sintética. El proceso es el siguiente:
Se divide el primer término del dividendo entre el primer término del divisor, lo que nos da un resultado de 4x^2.
Se multiplica el resultado anterior por el divisor (x – 2), lo que nos da 4x^3 – 8x^2.
Se resta el resultado anterior del dividendo (4x^3 + 2x^2 – 3x + 5), lo que nos da -6x^2 – 3x + 5.
Se divide el primer término del resultado de la resta anterior entre el primer término del divisor, lo que nos da -3x.
Se multiplica el resultado anterior por el divisor (x – 2), lo que nos da -3x^2 + 6x.
Se resta el resultado anterior del resultado anterior de la resta, lo que nos da -3x + 5.
El resultado final es 4x^2 – 3x + 5 / x – 2
Es importante notar que el proceso anterior se realiza hasta que el grado del polinomio resultante de la resta sea menor al grado del divisor. El residuo es el polinomio resultante de la resta. Es importante recordar que para dividir polinomios se utiliza la regla distributiva en cada uno de los términos del polinomio.